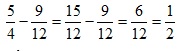NỐI ĐIỂM

Trên hai đường thẳng song song L1 và L2 người ta đánh dấu trên mỗi đường N điểm. Các điểm trên đường thẳng L1 được đánh số từ 1 đến N từ trái qua phải, còn các điểm trên L2 cũng được đánh số bằng p₁, p₂,…,p_N từ trái qua phải với p₁, p₂,…,p_N là một hoán vị của 1, 2,…,N. Hình vẽ dưới đây cho ví dụ từ 1 đến 9:

Ta gọi các số gán cho các điểm là số hiệu của chúng. Cho phép nối hai điểm trên hai đường thẳng có cùng số hiệu.

Yêu cầu: Tìm cách nối được nhiều cặp điểm nhất với điều kiện các đoạn nối không được cắt nhau.

Dữ liệu: vào từ tệp văn bản WIRES.INP

+ Dòng đầu chứa số nguyên dương N (N<=1000)

+ Dòng thứ hai chứa các số nguyên p₁, p₂,…,p_N các nhau bởi một ký tự trắng

Kết quả: ghi vào tệp văn bản WIRES.OUT

+ Dòng đầu tiên chứa k là số lượng các đoạn nối tìm được

+ Dòng tiếp theo chứa k số hiệu của các đầu mút của các đoạn nối (nếu có nhiều cách thì chỉ cần đưa ra một cách bất kỳ)

Ví dụ:

WIRES.INP	WIRES.OUT
9 2 5 3 8 7 4 6 9 1	5 2 3 4 6 9

BIẾN ĐỔI XÂU

Nguồn: https://traitaodo.wordpress.com

Cho xâu kí tự A, xét 3 phép biến đổi :
– Insert(i, C): i là vị trí, C là ký tự: Phép Insert chèn ký tự C vào sau vị trí i của xâu A.
– Replace(i, C): i là vị trí, C là ký tự: Phép Replace thay ký tự tại vị trí i của xâu A bởi kí tự C.
– Delete(i): i là vị trí: Phép Delete xóa ký tự tại vị trí i của xâu A.
Cho trước xâu A, hãy tìm một số ít nhất các phép biến đổi trên để biến xâu A thành xâu B.
Input :
– Dòng đầu ghi xâu A.
– Dòng 2 ghi xâu B.
Mỗi xâu có độ dài không quá 1000 ký tự.
Output :
– Dòng đầu ghi số phép biến đổi ít nhất
– Các dòng tiếp theo ghi cụ thể các bước biến đổi.

The Values You Can Make

Nguồn: http:/codeforces.com

Pari wants to buy an expensive chocolate from Arya. She has n coins, the value of the i-th coin is c_i. The price of the chocolate is k, so Pari will take a subset of her coins with sum equal to k and give it to Arya.

Looking at her coins, a question came to her mind: after giving the coins to Arya, what values does Arya can make with them? She is jealous and she doesn't want Arya to make a lot of values. So she wants to know all the values x, such that Arya will be able to make xusing some subset of coins with the sum k.

Formally, Pari wants to know the values x such that there exists a subset of coins with the sum k such that some subset of this subset has the sum x, i.e. there is exists some way to pay for the chocolate, such that Arya will be able to make the sum x using these coins.

Input

The first line contains two integers n and k (1  ≤  n, k  ≤  500) — the number of coins and the price of the chocolate, respectively.

Next line will contain n integers c₁, c₂, ..., c_n (1 ≤ c_i ≤ 500) — the values of Pari's coins.

It's guaranteed that one can make value k using these coins.

Output

First line of the output must contain a single integer q— the number of suitable values x. Then print q integers in ascending order — the values that Arya can make for some subset of coins of Pari that pays for the chocolate.

Examples

Input	Output
6 18 5 6 1 10 12 2	16 0 1 2 3 5 6 7 8 10 11 12 13 15 16 17 18
3 50 25 25 50	3 0 25 50

Tóm tắt đề: cho một dãy gồm N số và 1 số nguyên K

đề bảo ta rằng : Trong toàn bộ tập hợp có tổng = k

thì in ra tổng các tập hợp con của tập hợp đó

Knights in Chessboard

Nguồn: http://lightoj.com:81

Given an m x n chessboard where you want to place chess knights. You have to find the number of maximum knights that can be placed in the chessboard such that no two knights attack each other.

Those who are not familiar with chess knights, note that a chess knight can attack 8 positions in the board as shown in the picture below.

Input

Input starts with an integer T (≤ 41000), denoting the number of test cases.

Each case contains two integers m, n (1 ≤ m, n ≤ 200). Here m and n corresponds to the number of rows and the number of columns of the board respectively.

Output

For each case, print the case number and maximum number of knights that can be placed in the board considering the above restrictions.

Input	Output
3 8 8 3 7 4 10	Case 1: 32 Case 2: 11 Case 3: 20

Tóm tắt đề:

Cho bàn cờ vua kích thước nxm. Hãy tìm cách đặt quân mã lên bàn cờ vua sao cho các quân mã không ăn nhau và số lượng quân mã đặt được là lớn nhất

BỘ SỐ PY – TA – GO

Một bộ ba số tự nhiên được gọi là bộ số Py-ta-go nếu thỏa mãn điều kiện : bình phương một số bằng tổng bình phương hai số còn lại.

Ví dụ: Bộ số (3, 4, 5) là một bộ số Pytago vì : 5²=3²+4².

Yêu cầu: Cho số nguyên dương N. Hãy phân tích N thành tổng của một bộ Pytago

Dữ liệu vào: Từ tệp PYTAGO.INP chứa số nguyên N (1≤N≤10⁶)

Kết quả ra:  ghi vào tệp PYTAGO.OUT số lượng bộ số Pytago tách được

Ví dụ :

PYTAGO.INP	PYTAGO.OUT	Giải thích
30	1	132=52+122

Tính sai

Nguồn bài: http://vn.spoj.com/problems/WCALC/

Khi còn bé, các bạn học sinh học được cách trừ phân số bằng cách quy đồng mẫu số, rồi mới thực hiện phép trừ:  

Nhưng một lần, An tính thử hiệu hai phân số bằng cách lấy hiệu hai tử số và hiệu hai mẫu số và thấy thật ngạc nhiên là kết quả vẫn đúng: 

An thấy tính chất này thật kỳ diệu và An muốn biết, với phân số cho trước, có bao nhiêu cặp giá trị  a>=0 và m>=0 sao cho: 

Dữ liệu vào: từ tệp văn bản WCALC.INP: Một dòng chứa hai số nguyên dương b và n cách nhau ít nhất một dấu cách (1 <= b, n <= 10^6; trong 50% số test b, n <= 1000).

Dữ liệu ra: ghi vào tệp văn bản WCALC.OUT một số nguyên duy nhất là số lượng cặp (a,m) tính được.

Ví dụ:

WCALC.INP	WCALC.OUT
9 12	5

NHÀ CỦA ANDREW

Alpha là một làng đồi núi rộng lớn. Những ngôi nhà ở đây đều dựa lưng vào núi và hướng mặt tiền ra phía ngoài tạo nên thế chắc chắn và thoáng mát cho ngôi nhà, trước mỗi nhà là một cái sân rộng lớn cho bọn trẻ con chơi đùa và cũng là nơi để người dân phơi khô các nông sản mà họ làm được. Nhà của Andrew cũng được làm theo cấu trúc như vậy, mọi công việc chính đã xong, bây giờ chỉ còn mỗi lối đi từ nhà xuống đường chính. Andrew muốn đóng hai bên lối đi, mỗi bên là một dãy cọc bằng gỗ sao cho độ cao được sắp xếp theo chiều tăng dần. Do thiếu cọc nên Andrew phải lên rừng để tìm, trong khi đó ở nhà, bạn bè của Andrew không hiểu ý nên đã đóng các cọc này trên 1 hàng và không theo thứ tự nào cả. Lúc trở về Andrew quyết định nhổ đi một số cọc sao cho các cọc còn lại có chiều cao tăng dần. Hãy giúp Andrew tìm ra những cọc cần nhổ sao cho số cọc phải nhổ lên là ít nhất. Biết rằng có N chiếc cọc đã được đóng, chiều cao của mỗi cọc là a_i.

Dữ liệu vào: từ file ANDREW.INP

+ Dòng đầu tiên là số nguyên dương N (04

)

+ Dòng thứ hai chứa N số nguyên dương a_i trong đó số thứ i là chiều cao của cọc thứ i (1≤a_i≤10⁸)

Dữ liệu ra: ghi vào file ANDREW.OUT gồm 1 số duy nhất số lượng các cọc ít nhất phải nhổ lên.

Ví dụ:

ANDREW.INP	ANDREW.OUT
7 1 7 2 6 5 8 9	2

Các cọc được nhổ lên là cọc thứ 2 và thứ 4 (giá trị bằng 7 và 6)